declaration des variables en java exercices corrigés - débutant - initiation java

Série Exercices JAVA : Niveau débutant

Repérer les instructions de déclaration, observer la syntaxe d’une instruction

Exercice 1 : 

Observez ce qui suit, et indiquez ce qui est ou n’est pas une déclaration et ce qui est ou n’est pas valide :



a.     int i, j, valeur ;
b.     limite - j = 1024 ;
c.     val = valeur / 16 ;
d.     char char ;
e.     j + 1 ;
f.      int X ;
g.     float A ;
h.     A = X / 2 ;
i.      X = A / 2 ;
j.      X = X / 2 ;

Exercice 2 :

Comprendre le mécanisme de l’affectation

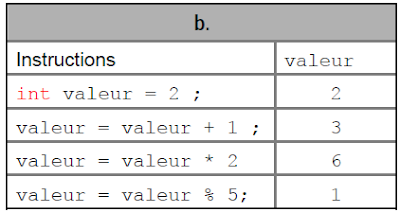
Quelles sont les valeurs des variables A, B, C après l’exécution de chacun des extraits de programme suivants :

Exercice 3:

Quelles sont les valeurs des variables a, b et c, valeur, x, y et z, après l’exécution de chacune des instructions suivantes :

Comprendre le mécanisme d’échange de valeurs

Exercice 4 :

Dans chacun des cas, quelles sont les valeurs des variables a et b après l’exécution de chacune des instructions suivantes :

Exercice 5 :

Laquelle des options suivantes permet d’échanger les valeurs des deux variables a et b ?

a = b ; b = a ;
t = a ; a = b ; b = t ;
t = a ; b = a ; t = b ;

Exercice 6 :

Soit trois variables a, b et c (entières). Écrivez les instructions permutant les valeurs, de sorte que la valeur de a passe dans b, celle de b dans c et celle de c dans a. N’utilisez qu’une (et une seule) variable entière supplémentaire, nommée tmp.

Exercice 7 :

Quel est l’effet des instructions suivantes sur les variables a et b (pour vous aider, initialisez a à 2 et b à 5) :

a = a + b ;
b = a – b ;
a = a – b ;

Calculer des expressions mixtes en java

Exercice 8 :

Donnez les valeurs des expressions suivantes, sachant que i et j sont de type int et x et y de type double (x = 2.0, y = 3.0) :

a. i = 100 / 6 ;
b. j = 100 % 6 ;
c. i = 5 % 8
d. (3 * i - 2 * j) / (2 * x - y)
e. 2 * ((i / 5) + (4 * (j - 3)) % (i + j - 2))
f. (i - 3 * j) / (x + 2 * y) / (i - j)

Exercice 9 :

Donnez le type et la valeur des expressions suivantes, sachant que n, p, r, s et t sont de type int (n = 10, p = 7, r = 8, s = 7, t = 21) et que x est de type float (x = 2.0f ) :

Comprendre le mécanisme du cast

Exercice 10 :

Soit les déclarations suivantes :

int valeur = 7, chiffre = 2, i1, i2 ;
float f1, f2 ;

Quelles sont les valeurs attribuées à i1, i2, f1 et f2 après le calcul de :

i1 = valeur / chiffre ;
i2 = chiffre / valeur ;
f1 = (float) (valeur / chiffre) ;
f2 = (float) (valeur / chiffre) + 0.5f ;
i1 = (int) f1 ;
i2 = (int) f2 ;
f1 = (float) valeur / (float) chiffre ;
f2 = (float) valeur / (float) chiffre + 0.5f ;
i1 = (int) f1 ;
i2 = (int) f2 ;


--------------------------------------------------------------

Correction  - Solution 

--------------------------------------------------------------

Solution Exercice 1 : 

a. Déclaration de trois entiers nommés i, j, valeur ;
b. Opération non valide, pas d'opérateur à gauche de l'affectation ;
c. Instruction d'affectation, pas de déclaration
d. Déclaration non valide, une variable ne peut s'appeler char
e. Opération non valide, ce n'est pas une instruction ;

f. Déclaration d'un entier nommé X ;
g. Déclaration d'un réel simple précision, nommé A ;
h. Affectation, pas une déclaration ;
i. Affectation non valide, un float ne peut être affecté à un entier ;
j. Affectation, pas une déclaration ;

Solution Exercice 2 : 

Solution Exercice 3 : 

Solution Exercice 4 : 

Solution Exercice 5 : 

Les instructions a = b ; b = a ; ne permettent pas l'échange de valeurs puisque la valeur contenue dans la variable a est perdue dès la première instruction (voir exercice 1-4, ci-dessus).

Les instructions t = a ; a = b ; b = t ; permettent l'échange des valeurs entre a et b, puisque la valeur de a est mémorisée dans la variable t, avant d'être effacée par le contenu de b.

Les instructions t = a ; b = a ; t = b ; ne permettent pas l'échange des valeurs car, la première instruction mémorise le contenu de la variable a, alors la seconde instruction efface le contenu de b.

Solution Exercice 6 : 

tmp = c ; c = b ; b = a ; a = tmp;

Solution Exercice 7 : 

Partant de a = 2 et b = 5, nous obtenons a = 5 et b = 2. Ainsi, grâce à ce calcul, les valeurs de a et b sont échangées sans utiliser de variable intermédiaire.

Solution Exercice 8 : 

a. i = 16 i est un entier, le résultat de la division est donc un entier ;

b. j = 4 4 est le reste de la division entière de 100 par 6 ;

c. i = 5 5 est le reste de la division entière de 5 par 8 ;

d. (3 * 5 – 2 * 4) / (2 * 2.0 – 3.0) ⇒ (15 – 8) / (4.0 – 3.0)
⇒ (7) / (1.0) ⇒ 7.0

e. 2 * ((5 / 5) + (4 * (4 – 3)) % (5 + 4 – 2) ⇒ 2 * 5 % 7

⇒ 10 % 7 ⇒3

f. (5 – 3 * 4) / ( 2.0 + 2 * 3.0) / (5 – 4) ⇒ (5 – 12) / (2.0 + 6.0) / 1
⇒ -7 / 8.0 ⇒ -0.875

Solution Exercice 9 : 

a.

x + n % p ⇒ 2.0f + 10 % 7 ⇒ 2.0f + 3 ⇒ 5.0f
x + n / p ⇒ 2.0f + 10 / 7 ⇒ 2.0f + 1 ⇒ 3.0f
(x + n) / p ⇒ (2.0f + 10) / 7 ⇒ 12.0f / 7 ⇒ 1.7142857f
5. * n ⇒ 5. * 10 ⇒ 50.0f
(n + 1) / n ⇒ (10 + 1) / 10 ⇒ 11 / 10 ⇒ 1
(n + 1.0) / n ⇒ (10 + 1.0) / 10 ⇒ 11.0 / 10 ⇒ 1.1
r + s / t ⇒ 8 + 7 / 21 ⇒ 8 + 0 ⇒ 8

b.

r + t / s ⇒ 8 + 21 / 7 ⇒ 8 + 3 ⇒ 11
(r + t) / s ⇒ (8 + 21) / 7 ⇒ 29 / 7 ⇒ 4
r + t % s ⇒ 8 + 21 % 7 ⇒ 8 + 0 ⇒ 8
(r + t) % s ⇒ (8 + 21) % 7 ⇒ 29 % 7 ⇒ 1
r + s / r + s ⇒ 8 + 7 / 8 + 7 ⇒ 8 + 0 + 7 ⇒ 15
(r + s) / (r + s) ⇒ (8 + 7) / ( 8 + 7) ⇒ 15 / 15 ⇒ 1
r + s % t ⇒ 8 + 7 % 2 ⇒ 8 + 7 ⇒ 15

Solution Exercice 10 : 

i1 = valeur / chiffre ⇒ 7 / 2 ⇒ 3
i2 = chiffre / valeur ⇒ 2 / 7 ⇒ 0
f1 = (float) (valeur / chiffre) ⇒ (float) (7 / 2) ⇒ (float) 3 ⇒ 3.Of
f2 = (float) (valeur / chiffre) + 0.5f ⇒ 3.0f + 0.5f ⇒ 3.5f
i1 = (int) f1 ⇒ (int) 3.0f ⇒ 3
i2 = (int) f2 ⇒ (int) 3.5f ⇒ 3
f1 = (float) valeur / (float)chiffre ⇒ 7.0f / 2.0f ⇒ 3.5f
f2 = (float) valeur / (float)chiffre + 0.5f ⇒ 3.5f + 0.5f ⇒ 4.0f
i1 = (int) f1 ⇒ (int) 3.5f ⇒ 3
i2 = (int) f2 ⇒ (int) 4.0f ⇒ 4