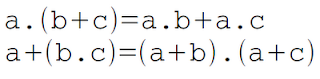TD Algèbre de Boole cours exercices corrigés

Algèbre de Boole

Système algébrique constitué de l'ensemble { 0, 1 }

• Variable booléenne : variable qui prend une valeur 0 ou 1

Trois opérateurs de base

NON / NOT

• Inverse/complémente la valeur de la variable a

ET / AND ( a.b ou ab )

• Retourne 1 si a et b sont à 1, sinon retourne 0

OU / OR ( a + b )

• Retourne 1 si a ou b est à 1, sinon retourne 0

Origine

• Mathématicien anglais Georges Boole, 1815 – 1864

Propriétés de base

Involution :

Idempotence :

Complémentarité :

Éléments neutres :

Absorbants :

Associativité :

Distributivité :

Règles de De Morgan :

Optimisations :

Fonction logique

Fonction logique

• Prend en entrée une ou plusieurs variables booléennes
• Retourne une valeur booléenne fonction des variables d'entrée

Définition d'une fonction logique : deux méthodes

•  Par son expression logique
• Combinaison des variables de la fonction via les opérateurs de base de l'algébre de boole
• Exemple : fonction f de trois variables a, b et c

• Par sa table de vérité
• Table qui définit la valeur de la fonction pour chaque combinaison de valeurs possibles en entrée

Tables de vérité

Table de vérité pour une fonction à p variables

• Pour chacune des combinaisons différentes de p valeurs, préciser le résultat de la fonction

Table de vérité des opérateurs de base

Fonction logique

Equivalence/passage entre expression logique et la table de vérité de la fonction

• On peut toujours déterminer l'une à partir de l'autre

Deux fonctions logiques sont identiques si

• On peut montrer via les propriétés de l'algèbre de Boole que leurs expressions logiques sont identiques
• Leurs tables de vérité sont identiques

Note :

Quand on parle de fonction logique, on parle souvent de la forme correspondant à l'expression logique

Formes canoniques d'une fonction

Pour une fonction logique à x variables

• Un minterme : groupe des x variables (pouvant être complémentées) liées par des ET
• Un maxterme : groupe des x variables (pouvant être complémentées) liées par des OU

Forme canonique d'une fonction logique

• Première forme : union (OU) de mintermes
• Second forme : intersection (ET) de maxtermes

Exemples de formes canoniques

Fonction à 3 variables a, b et c, exemples :

• Mintermes :

• Maxtermes :

• Première forme canonique :

• Seconde forme canonique :

Passage aux formes canoniques

Partir de la fonction et la transformer pour faire apparaître des mintermes/maxtermes complets Pour la transformation

• On s'appuie sur les propriétés de l'algèbre de Boole, et notamment des invariants :

Exemple de passage à la première forme canonique

Exemple de passage à la seconde forme canonique

Passage de la fonction logique à la table de vérité

Pour chaque combinaison de valeurs possibles pour les variables, on détermine la valeur booléenne de f(X) (X = ensemble des variables)

Exemple :

Passage de la table de vérité à la fonction logique

A partir de la table de vérité : fonction sous première forme canonique

• Pour chaque valeur de f(X) égale à 1
• On définit un minterme de toutes les variables tel que
• Img
• La première forme canonique de f(X) est le OU de ces mintermes

A partir de la table de vérité : fonction sous seconde forme canonique

• Pour chaque valeur de f(X) égale à 0
• On définit un minterme de toutes les variables tel que

Exemple de calcul de la fonction logique sous première forme

A partir de la table de vérité de l'exemple précédent

• f(a,b,c) = 1 quand :

• On fait le OU de ces mintermes

Exemple de calcul de la fonction logique sous seconde forme

A partir de la table de vérité de l'exemple précédent

• f(a,b,c) = 0 quand :

 On fait le OU de ces mintermes

• Au final :

Minimisation des fonctions logiques

Les formes canoniques d'une fonction logique sont une définition correcte de la fonction, mais elles peuvent être simplifiées

• Pour écrire la même fonction avec le moins de termes et les plus simples possibles
• Pour réaliser la fonction avec moins d'éléments électroniques (portes logiques)

Deux méthodes pour simplifier l'écriture d'une fonction logique

• Utiliser les propriétés de l'algèbre de Boole
• Utiliser la méthode des tableaux de Karnaugh

Simplification via algèbre de Boole

A partir des propriétés de l'algèbre de Boole, transformer la fonction pour la simplifier Principes généraux

• Simplifier la fonction initiale à l'aide des propriétés de l'algèbre de Boole
• Appliquer la propriété d'involution

à la fonction simplifiée est parfois intéressant, mais calculs longs ...

• Essayer de déduire d'autres simplifications après chaque simplification

Exemple de simplification via algèbre de Boole

Exemple de simplification via algèbre de Boole

Simplification par la méthode des tableaux de Karnaugh

Principes généraux

• Représentation sous une forme particulière de la table de vérité d'une fonction logique
• Détermination des blocs rectangulaires de taille 2ⁿ (1, 2, 4, 8...) bits adjacents à 1
• On en déduit la fonction simplifiée associée à la table de vérité
• On représente un tableau à 2 dimensions
• Chaque dimension concerne une ou 2 variables
• Le passage d'une colonne à une colonne adjacente ou d'une ligne à une ligne adjacente modifie la valeur d'une seule variable
• Le tableau se referme sur lui-même : la colonne la plus à gauche est voisine de la colonne la plus à droite, idem pour les lignes du haut et du bas
• Pour les 2 colonnes (2 lignes) extrêmes, là aussi, une seule variable doit changer de valeur entre ces 2 colonnes (lignes)
• Une case du tableau contient une valeur booléenne, déterminée à partir de la table de vérité et des valeurs des variables

Regroupement en blocs rectangulaires des bits à 1 adjacents

• Tous les bits à 1 du tableau doivent être englobés dans au moins un bloc (un bloc à une taille de 1, 2, 4, 8 ... bits)
• Un bit à 1 peut appartenir à plusieurs blocs
• On doit créer les blocs les plus gros possibles

A chaque bloc correspond un terme formé comme suit

• Pour le bloc, si une une variable prend les valeurs 0 et 1, on ne la prend pas en compte
• On ne conserve que les variables qui ne varient pas. Si une variable a reste à 1 : on note a, si reste à 0 : on note a
• Le terme logique du bloc correspond au ET de ces variables qui ne changent pas

La fonction logique simplifiée est le OU de tous les termes des blocs trouvés

Exemple de tableau de Karnaugh

Table pour 2 variables

2 groupes de 2 bits adjacents :

• Pour le vertical : on a toujours a = 1 donc cela donne le terme a
• Pour l'horizontal : idem mais avec b
• f(a,b) = a + b

Table pour 3 variables

Bloc le plus petit : a = 0, b = 0, c = 1

• Donne le terme

Mais simplification pas suffisante

• La table se referme sur elle-même
• On doit également regrouper en bloc les plus grands possibles mêmes si des bits appartiennent à plusieurs blocs
• Le bit seul à gauche doit donc être regroupé avec la case a=1,b=0,c=1 à droite en bas de la table

• Au final pour ce bloc, on a donc :

Bloc le plus gros : a reste à 1, b passe de 0 à 1 et c passe de 0 à 1

On ne conserve que les variables qui ne changent pas. Donc on a le terme : a

Au final :

Pourquoi pour le bloc de 4 on obtient juste a ?

• Si on fait le OU de tous les mintermes pour lequel la valeur est 1, cela donne pour ce bloc de 4 :

• Les variables d'un bloc prenant les valeurs de 0 et 1 sont donc systématiquement non significatives

Exemple de tableau de Karnaugh

Tableau pour 4 variables

• On doit là aussi regrouper en les plus gros blocs possibles même si on recoupe d'autres blocs
• La table se referme sur elle-même