Exercices Corrigés circuits logiques QCM-AND-NAND-OR-XOR-NOT - TP additionneur - TD théorèmes Morgan et solution
Les composants électroniques de base
Nous allons faire un petit TD de mise en application sur les opérateurs logiques.
Objectif
L’objectif est de comprendre comment à partir de simples transistors on peut fabriquer un composant aussi complexe qu’un microprocesseur. C’est aussi un moyen de vous familiariser avec la logique booléenne. C’est une compétence qui vous servira en mathématiques et en programmation.
Exercice 1
On vous fournit le circuit suivant :
1. Comment s’appelle le composant noté P ?
2. Donnez les tables de vérité en sortie de chaque composant, en vous inspirant du tableau suivant (j’ai commencé à le remplir) :
3. Simplifiez la table de vérité grâce au tableau ci-dessous, puis indiquez à quel composant étudié dans le cours correspond cette table et dessinez son symbole.
Exercice 2
Le demi-additioneur (half adder)
1. Addition en binaire. Remplissez le tableau suivant :
La dernière opération génère une ________________.
2. Comment s’appellent les deux composants représentés sur le schéma ?
3. Donnez la table de vérité de l’ensemble.
Exercice 3
L’additionneur complet (full adder)
Imaginons que l’on additionne deux nombres binaires composés de plusieurs bits. On additionne chaque bit individuellement avec un demi-additionneur mais il faut tenir compte de la retenue issue de l’opération précédente. Un électronicien aboutirait au circuit suivant :
Note : CIN représente la retenue précédente et COUTreprésente la retenue issue du calcul.
1. Comment s’appelle le composant en bas à droite.
2. Donnez la table de vérité en sortie de chaque composant.
Exercice 4
Les théorèmes de De Morgan
Je profite de cette séquence sur les opérateurs logiques pour vous présenter un moyen de simplifier certaines expressions logiques. Si l’on applique les théorèmes de De Morgan :
• NON(A ET B) peut s’écrire NON A OU NON B
• NON(A OU B) peut s’écrire NON A ET NON B
Prenons un exemple.
NON((NON(A ET B) OU NON (C ET D)) peut s’écrire
NON((NON A OU NON B) OU (NON C OU NON D)) peut s’écrire
NON(NON A OU NON B) ET NON(NON C OU NON D) peut s’écrire
NON(NON A) ET NON(NON B) ET NON(NON C) ET NON(NON D) peut s’écrire
A(*) ET B ET C ET D
Mettons en application immédiatement.
1. Simplifiez l’expression : A OU NON (B ET NON C)
2. Vous trouverez de nombreuses applications de ces théorèmes en programmation.
Imaginons que l’on ait un bout d’algorithme qui contienne ceci :
SI NON(PRIX = 100 ET QUANTITE > 50) ALORS …
Simplifiez cette expression logique. Je ne veux plus voir de NON à la fin, réfléchissez donc bien à la signification du NON
(*) La double négation NON(NON A) peut se simplifier en A, de même qu’en français dire « je ne dis pas qu’il ne faut pas travailler son cours » signifie « je dis qu’il faut travailler son cours ».
QCM d’auto-évaluation
1. Ce symbole représente :
a) un inverseur
b) une porte NOR
c) un interrupteur
d) un transistor
2. Pour chaque symbole, indiquez le nom qui lui correspond :
a) Porte NAND
b) Porte AND
c) Porte NOR
d) Porte XOR
e) Porte OR
f) Porte NOT
3. Le fonctionnement d’un transistor peut être assimilé à celui de :
a) un annulateur
b) un commutateur
c) un interrupteur
d) un cavalier (jumper)
4. Lorsque le transistor est conducteur, il est dit :
a) bloqué
b) saturé
c) fermé
d) commuté
5. Complétez la phrase :
Une porte NAND est constituée de deux ____________________ montés en ____________________, alors qu’une porte NOR est constituée de _____ transistors montés en ______________________.
6. Pour chaque table de vérité, indiquez le nom de l’opérateur auquel elle correspond :
a) NAND
b) AND
c) OR
d) XOR
e) OR
f) NOT
7. Le montage ci-dessous correspond à :
a) une porte OR
b) une porte NOR
c) une porte AND
d) une porte NAND
8. Selon De Morgan, l’expression NON (A ET B) se simplifie en :
a) NON A ET NON B
b) A NON ET B
c) NON A OU NON B
d) NON A ET B
Correction des exercices circuits logiques - électroniques
-------------------------------------------------------------------------------------------------Solution de l'exercice 1 :
1. C’est une porte NAND (comme un AND mais avec un petit rond au bout symbolisant la négation). Je vous rappelle que vous devez être capable de reconnaître visuellement les portes logiques.
2. Il faut traiter le circuit de gauche à droite. On observe que A et B sont les deux entrées du circuit, dont on examine les 22 possibilités. On commence par S1 qui correspond à A NAND B.
Ensuite, connaissant S1 on peut examiner S2 qui n’est autre que A NAND S1 et ainsi de suite.
3. De la colonne S, vous devez reconnaître qu’il s’agit d’une porte XOR, que l’on peut donc réaliser (comme je vous l’ai dit d’ailleurs dans le cours) avec quatre portes NAND.
Solution de l'exercice 2 :
Le demi-additioneur (half adder)
1. Addition en binaire. Remplissez le tableau suivant :
La dernière opération génère une retenue.
2. Celui du haut est une porte XOR, celui du bas est une porte AND.
3. Vous devez vous même constituer la table de vérité. Il faut s’inspirer des autres exercices et de la méthodologie donnée dans le cours. Reprenons :
1. On a deux entrées
2. On a deux sorties
3. On a donc quatre colonnes dans la table de vérité
4. On a 22 lignes puisqu’on a deux entrées
Ensuite, on construit la table que l’on va compléter avec A XOR B pour la colonne Sum et A AND B pour la colonne Carry (*) :
Oui, il s’agit bien de l’additionneur 1 bit première version étudié dans le cours.
(*) Carry signifie retenue en anglais.
Solution de l'exercice 3 :
L’additionneur complet (full adder)
1. C’est une porte OR.
2. Pour la table de vérité, vous avez un premier travail préparatoire à effectuer : nommer les sorties de chaque composant afin de pouvoir ensuite construire le tableau.
Nous avons trois entrées à gauche et cinq sorties. Nous aurons donc un tableau à 8 colonnes et 23 lignes :
Mine de rien, vous commencez à savoir compter en binaire. En effet, les colonnes A, B et CIN
contiennent tous les nombres binaires de 0 à 7. De plus, vous commencez à faire des calculs en
binaire (on travaille sur un additionneur !). Lisons le tableau, par exemple sur la dernière ligne :
Cela veut dire que lorsque l’on fait le calcul 1 + 1 + 1, le résultat est 11 en binaire (ce qui fait 3 en base décimale). Je vous dis ça parce que c’est l’objet de la prochain séquence de cours.
Solution de l'exercice 4 :
1. A OU NON (B ET NON C) peut s’écrire :
A OU (NON B OU NON (NON C))
A OU (NON B OU C) <-- conservez la parenthèse
2. SI NON(PRIX = 100 ET QUANTITE > 50) ALORS … peut s’écrire
SI NON(PRIX = 100) OU NON(QUANTITE >50) ALORS … peut s’écrire
SI PRIX ! 100 OU QUANTITE <= 50 ALORS …
Faites bien attention : le contraire de « supérieur à » est « inférieur ou égale à ».
Correction QCM:
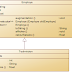
Question
|
Réponse
|
1
|
D
|
3
|
C
|
4
|
B
|
7
|
A
|
8
|
C
|
2. Pour chaque symbole, indiquez le nom qui lui correspond :
5. Complétez la phrase :
Une porte NAND est constituée de deux transistors montés en série, alors qu’une porte NOR est constituée de deux transistors montés en parallèle.
6. Pour chaque table de vérité, indiquez le nom de l’opérateur auquel elle correspond :
Cours sur les circuits logiques - composants électroniques
Article plus récent Article plus ancien